Now that we have seen two basic examples of binary search we are going to generalize it and see how it can be applied to solve more complicated problems.
Let's start by rewriting the integerSqrt as follows:
static int integerSqrt(int n) {
int L = 0;
int R = n + 1;
while(R - L >= 2) {
int M = (L + R) / 2;
if(check(M, n)) L = M; // dismiss all values < M
else R = M; // dismiss all values > M
}
return L;
}
static boolean check(long x, int n) {
return x * x <= n;
}
It is essentially the same code, except that we extracted the check condition. When we read it like that we can see that what the code is doing is finding the maximum value such that the condition check is true. And it will work because check has the following property:
When we vary \(x\), it is always true until some point and then always false after that point. We call such a property a monotone property.
The following image illustrates this:

This means that we can actually use binary search to solve any problem in which we seek the largest value that satisfies some given property as long as that truth value of that property is monotone.
We can thus generalize the code as follows:
// find the largest index where check is true
static int binarySearch(int n) {
int L = 0;
int R = n + 1;
while(R - L >= 2) {
long M = (L + R) / 2;
if(check(M)) L = M; // dismiss all values < M
else R = M; // dismiss all values > M
}
return L;
}
static boolean check(int M) {
// TODO: the condition you need to check
}
Let's illustrate this on a real problem.
Plane purchase problem:
You want to purchase a plane to travel around the world.
You know the positions \((x_i, y_i)\) of all \(n \leq 1000\) airports on which you are allowed to land. The cost of the planes is proportional to the maximum distance that it can travel. Therefore, you would like to know what is the minimum travel distance that a plane needs to be able to travel so that you can travel between any two airports.
The are only planes for sale that travel integral distances. That is, you can purchase a plane able to travel any positive integer distance but only those. For instance, you cannot but a plane with maximum travel distance, say, \(1.5\) or \(\sqrt{2}\).
Note that by travel we do not mean a direct flight, you don't mind to have to stop in some airports on the way to refuel your plane.
At first sight, this problem might seem like an intimidating geometry problem but when you think about it, but it turns out that it can easily be solved using binary search on the answer.
For example, imagine that the airports are located at the black dots shown in the figure.
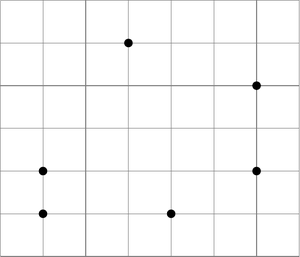
With a place capable of traveling distance \(3\) it is possible to travel between the airports that are connected by a thick line in the following figure:
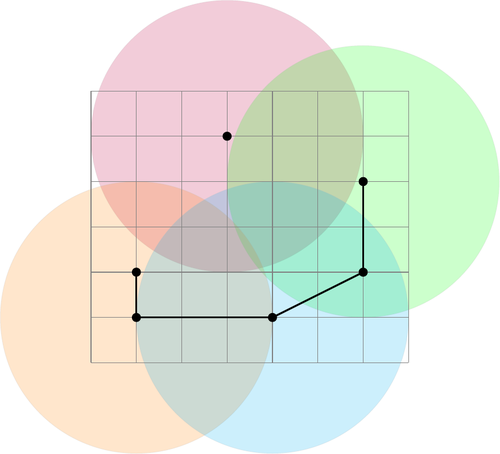
As we can see, distance \(3\) is not enough to reach the top airport. With a plane capable of traveling distance \(4\) it becomes possible to reach the top airport:
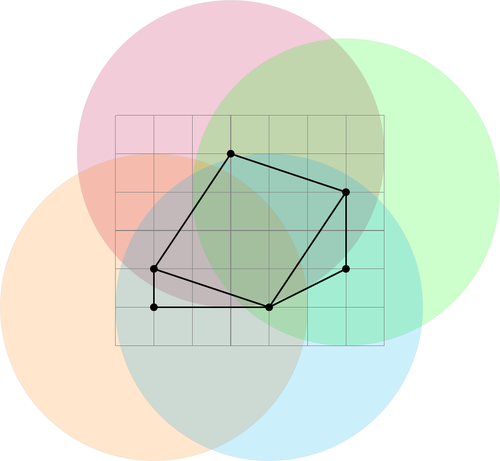
It is clear that if one distance is not enough, then all smaller distances are also not enough. Thus we can do a binary search on the answer to find the smallest distance for which the it becomes possible to travel between any two airports.
So the problem becomes: given a distance \(d\), is it possible to travel (directly on indirectly) between any two airports?
This is a huge simplification of the problem, before we needed to solve:
Find the minimum distance \(d\) for which traveling is possible.
Now we simply need to solve:
Given a plane able to travel distance \(d\), is it possible to reach every airport?
Since \(n \leq 1000\), a \(O(n^2)\) algorithm is fast enough. We can thus check the condition by building the graph corresponding to the given \(d\) and using a graph traversal algorithm to check whether the graph is connected.
Note: In this problem we seek the smallest \(d\) such that some condition holds whereas the above code finds the largest value such that some condition holds as shown in the following image:

The easiest way to adapt the code is to negate your check condition so that it returns true if \(d\) is not enought and false otherwise. Then the answer will be the output of the binary search plus \(1\):
// find the smallest index where check is true
static int binarySearch(int n) {
int L = 0;
int R = n + 1;
while(R - L >= 2) {
long M = (L + R) / 2;
if(!check(M)) L = M; // dismiss all values < M
else R = M; // dismiss all values > M
}
return L + 1;
}
static boolean check(int M) {
// TODO: the condition you need to check
}
 INGInious
INGInious