In this section we will discuss some theoretical aspects of DP a bit further.

Underlying a DP problem there is a state graph. The nodes of this graph are the states defined for the problem. There is a directed edge from state \(s_1\) to \(s_2\) if \(s_2\) directly depends on \(s_1\) in the recurrence relation.

To illustrate this, let's go back to the bottom-up knapsack example. The recurrence relation was:

Thus both \((i - 1, c - w_i)\) and \((i - 1, c)\) will have an edge to \((i, c)\). The following figure illustrates this.

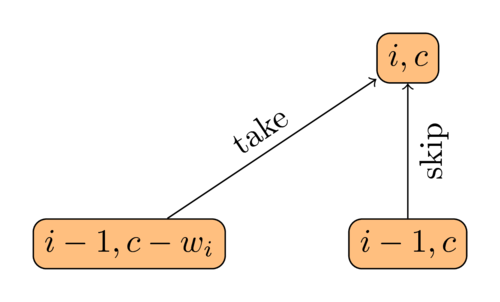
To show a complete example, imagine that we have \(5\) items with weights \([1, 3, 3, 2, 4]\) and values \([1, 4, 2, 3, 5]\) to put on a knapsack of capacity \(10\). Then, with the above formulation, the state space graph is the following:

We claim that this graph does not contain any cycles. We encourage you to think about why this is true before reading further.

The reason why this graph is acyclic is that the first coordinate of each node, the object index, is strictly increasing in any path of the graph.

This is a crucial property that our DP formulation must satisfy. If we happend to have cycles in the DP state graph, then the order of the subproblems is not well defined and the algorithm will loop forever because the answer to some subproblems will depend on itself.

The state graph of a DP formulation MUST be acyclic!

To better illustrate this consider the shortest path problem. Given a graph \(G\) with positive edge weights and a node \(s\) we want to compute the shortest path length from \(s\) to each other node. Let's have a state for each node \(v\) of the input graph and define DP subproblems as follows:

Clearly \(dp(s) = 0\) since the shortest path from \(s\) to itself is the empty path (we just stay where we are). Otherwise, to reach \(v\), we will have to go from \(s\) to some node \(u\) that is connected to \(v\) and then traverse edge \((u, v)\). But since we want a shortest path to reach \(v\), of course we will use a shortest path to reach \(u\) as the following figure illustrates.

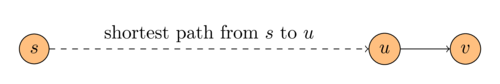
This means that we reduced the problem \(dp(v)\) of computing the shortest path to \(v\), to the problem of computing the shortest path to each in-neighbour \(u\) of \(v\).

We then write the following recurrence relation:

What does the state graph for this DP formulation look like? Think about it for a while.

It is exactly the input graph \(G\) !

In this case, a state is simply a node of the graph so clearly both graphs have the same set of nodes. But they also have the same set of edges since two states \(u\) and \(v\) are related to each other in the recurrence relation if and only if there is an edge from \(u\) to \(v\) in \(G\).

This means, according to what we said above, that this DP formulation will work if and only if the input graph \(G\) is acyclic.

We will see later when we study the Bellman-Ford algorithm how we can, at the cost of having more states, change the state formulation in order to break cycles and get a general shortest path algorithm.