The algorithm that we presented in the maxflow task is due to Jack Edmonds and Richard Karp and thus named Edmonds-Karp. The idea of finding paths in the residual graph was already known. Their contribution was to show that the algorithm runs in polynomial time if we use BFS to find the paths. This class of algorithms is called augmenting path algorithms.
In general, it is easy to find an upper bound for the running time of an augmenting path algorithm:
Whenever we are able to find a path, we push at least one new unit of flow. Therefore the total flow is strictly increasing so that we will perform at most \(F\) pathfinding iterations, where \(F\) is the maximum flow. Thus the complexity is \(O(F (V + E))\) if we use an \(O(V + E)\) algorithm to find the path such as DFS of BFS.
However, this is not very good news as we usually do not want the complexity to depend on the value of the answer since it could mean that even on a very small graph with, say \(F = 10^{10}\), the algorithm would take forever to run.
We are going to show that if we use BFS to find the paths, the complexity will be \(O(V E^2)\).
The remainder of this section is quite theoretical. So, if anything, the take-home messages are that:
- An augmenting path algorithm to compute the maximum flow will make at most \(F\) path computations.
- Using BFS we can bound the number of path computations to \(O(VE)\).
Theorem
During the execution of the algorithm, the distances of the nodes from the source never decrease.
PROOF
Assume that, after pushing flow on a path, the distance of some node was decreased. Denote by \(d_{bef}\) the BFS distances and \(d_{aft}\) the distances after.
Let \(v\) be the closest node to the source \(s\) whose distance was decreased. That is \(v\) such that:
- \(d_{aft}(s, v)\) is minimum
- \(d_{aft}(s, v) < d_{bef}(s, v)\)
Let \(p = (s, \ldots, u, v)\) be the shortest path from \(s\) to \(v\) on the residual graph after that we pushed the flow.

Recall that in the BFS we ignore edges of capacity 0. Therefore it means that every edge of \(p\) has positive capacity.
By definition we have that
Since \(v\) is the closest node to \(s\) whose distance decreased and \(u\) is closer to \(s\) than \(v\), we know that the distance of \(u\) did not decrease. That is
We can now show that the capacity of (u, v) before was \(0\). If it was not, then it was considered by the BFS and thus, by the triangular inequality, \(d_{bef}(s, v) \leq d_{bef}(s, v) + 1\).
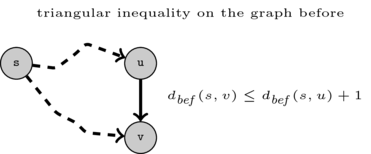
Therefore
This would contradict the fact that the distance of \(v\) was decreased.
So we have the following situation:
Before we pushed the flow, the capacity of \((u, v)\) was \(0\) but after it was not, since it is an edge of \(p\). The only way in which this is possible is if flow was pushed on the reverse edge \((v, u)\). Since we only push on shortest paths, we must have \(d_{bef}(s, u) = d_{bef}(s, v) + 1\). Hence
So that, \(d_{bef}(s, v) \leq d_{aft}(s, v)\) contradicting the fact that the distance to \(v\) decreased.
We are now going to use the fact that the distances never decrease to prove the time complexity of the algorithm.
Theorem
Edmonds-Karp algorithm performs at most \(O(VE)\) BFS's, that is, calls to
augmentFlowBFS.
PROOF
We say that an edge is critical if we push flow on a path \(p\) that contains it and that edge is a minimum capacity edge of that path. In other words, it is an edge that will have capacity \(0\) after we push flow on \(p\).
We are going to bound the number of times an edge can become critical. Let \((u, v)\) be any edge in the graph. Denote by \(d\) the BFS distances just before \((u, v)\) becomes critical. Since we find shortest paths to push flow we must have
After we push the flow, since \((u, v)\) is critical, it will have capacity 0. Thus, for it to become critical again, we must first push flow on the reverse edge \((v, u)\). Let \(d'\) denote the distances just before this happens. Again, we must have
Therefore, since distances cannot decrease, we have that \(d(s, v) \leq d'(s, v)\) and thus
We conclude that between two iterations where \((u, v)\) is critical the distance from s to u must increase by at least 2. Since the distances are at most \(V\), it means that each edge will become critical at most \(V / 2\) times. As there are \(E\) edges in total, the maximum number of times an edge can become critical overall is \(E V / 2 = O(VE)\). Since whenever we push flow on a path, that path must contain at least one critical edge, we conclude that the number of calls to augmentFlowBFS is \(O(VE)\).
Since the time complexity of BFS is \(O(V + E)\) we have the following theorem for the time complexity of Edmond-Karp maximum flow algorithm.
Theorem
Edmonds-Karp algorithm runs in \(O(VE^2)\)
 INGInious
INGInious