Simply put, a graph \(G\) is a set of objects \(n\) objects, usually the set \(\{ 0, \ldots, n - 1\}\), where some pairs of those objects are connected together. The set of objects is called the nodes of the graph and the connections are called edges. Usually the set of nodes is denoted by \(V(G)\) and the set of edges by \(E(G)\).

Example

A graph with \(5\) nodes and \(5\) edges \((0, 1), (1, 2), (2, 0), (2, 1)\) and \((4, 5)\).

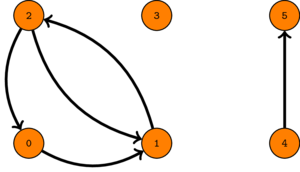
A edge \((u, v)\) represents the fact that we can go from node \(u\) to node \(v\).

The most classical example of problem that can be abstracted with graphs are connectivity problems. Suppose that the nodes represent airports and the edges represent direct flights between those airports. To find out whether it is possible to travel from some airport \(A\) to another airport \(B\) we can look in the corresponding graph if there is a sequence of nodes \((v_1, v_2, \ldots, v_k)\) such that:

1. For each pair of consecutive nodes, there is an edge in the graph. Formally this means that \((v_{i}, v_{i + 1}) \in E(G)\).
2. The sequence starts at \(A\) and ends at \(B\), that is, \(v_1 = A\) and \(v_k = B\).

Observe that in the graph, the geographic position of the airports is lost in the graph representation of the problem. We abstract all that information and keep only the relations between the airports. This is all we need to answer the question. When we draw the graph, the relative position of the nodes have no meaning, they are chosen only for readability.

But before we start solving problems on graphs, we need to find a way to represent them in the computer. There many alternative ways to do so but for now we will focus on a simple and easy-to-code representation and extend it later, when needed.

For each node we will simply keep a list of the nodes to which it is connected. Since the nodes are numbers from \(0\) to \(n - 1\), the simplest way is to use an array of lists, say \(g\), such that \(g[v]\) is a list of all edges starting at \(v\) and ending at some node \(u\).

Example

The above is represented by an array of size \(6\). The \(i\)-th element of the array is a list that contains all the neighbours of \(i\).

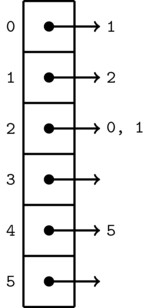
In java this can be done as follows:

LinkedList<Integer>[] g = new LinkedList[6];
for(int v = 0; v < g.length; v++) {
    g[v] = new LinkedList<>();
}
g[0].add(1);
g[1].add(2);
g[2].add(0);
g[2].add(1);
g[4].add(5);

This graph representation is suitable to traverse the whole graph to find a path because we can iterate over all outgoing edges of a node in linear time. Also, building the graph with this structure takes linear time \(O(n + m)\) since adding an element to a LinkedList is done in constant time.

// iterating over neighbours of v
for(int u : g[v]) {
  // do something
}

It is not suitable for checking whether two nodes are connected since executing a contains call on a list takes linear time. The same goes for deleting an edge.

If such operations are necessary one alternative is to use a TreeSet or HashSet instead of the list. The disadvantage is that looping on the neighbours of a node is not linear anymore neither is creating the graph.

Another alternative is to use an adjacency matrix. This means using a binary \(n \times n\) matrix \(A\) such that \(A[u][v]\) is \(1\) if and only if edge \((u, v) \in E(G)\). This makes it very easy to add and delete edges but takes quadratic time to create and traverse. Therefore it should be avoided, except in some specific cases that we will discuss later on.

For now we will stick with the list representation as it is enough for the most fundamental graph traversal algorithms.

For most problems the graphs are represented in the input by first giving a line with \(n\) and \(m\), the number of nodes and edges, respectively. Then \(m\) lines each with two integers representing the edges. The following code reads a graph represented in this way. You will need it in the following tasks.

@SuppressWarnings("unchecked")
public static void main(String[] args) {
     Scanner reader = new Scanner(System.in);
     int n = reader.nextInt();
     int m = reader.nextInt();
     LinkedList<Integer>[] g = new LinkedList[n];
     for(int i = 0; i < n; i++) {
         g[i] = new LinkedList<>();
     }
     for(int i = 0; i < m; i++) {
         int u = reader.nextInt();
         int v = reader.nextInt();
         g[u].add(v);
     }
     // do something with g
     reader.close();
}

The suppress warning is necessary in some contest environments as otherwise the code will give a compile error. In modern judging systems it is often not necessary. We put it just to be safe.

Note: In a lot of problems the nodes of the input graph are numbered from \(1\) to \(n\) rather than \(0\) to \(n - 1\). In this case the easiest solution is to simply subtract \(1\) while reading the input and add \(1\) while writing the output. This may seem obvious but I have seen students subtracting \(1\) in every access to \(g\) which is very annoying and time consuming.