Geometry - Point in convex polygon - Competitive Programming

Geometry - Point in convex polygon

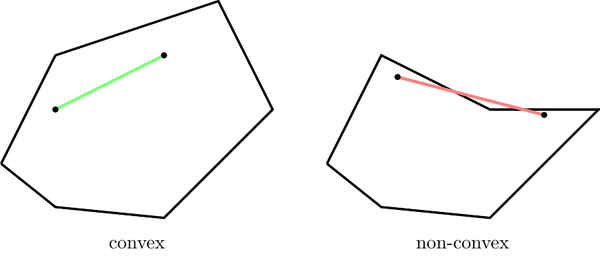
Another nice application of orientation is to check whether a point \(p\) lies inside a convex polygon.

A convex polygon is a simple polygon (with no self intersections) such that any line segment between two points inside of the polygon lies completely inside of it.

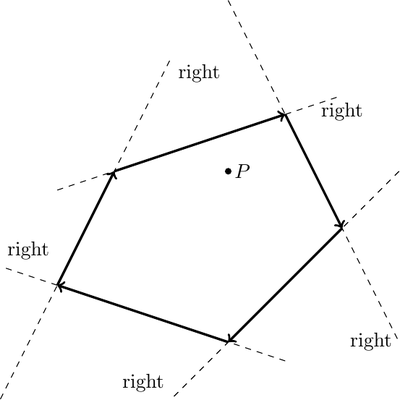
The point will be inside a convex polygon if and only if it lies on the same side of the support line of each of the segments. That is, either it lies on the left of every line or it lines on the right of every line.

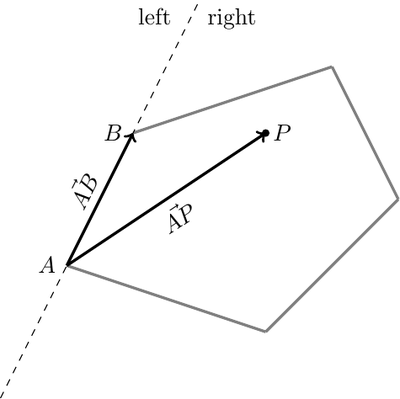
But we already know how to check whether a point lies on the right of left of a line defined by two points \(A\) and \(B\). For each polygon segment \(\overline{AB}\) we simply need to compute \(orient(A, B, P) = \vec{AB} \times \vec{AP}\) and check that they all have the same sign (which indicates the side).

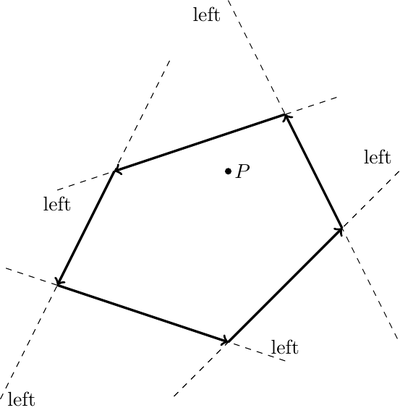
Note that the solution is not to whether the point lies to the right of each line but to check whether the point lies on the same side of each line. In the above example it will indeed be always on the right by this is because the polygon is oriented in a clockwise fashion. If it had been oriented in a counter-clockwise fashion, the point would have been on the left of each line as show in the following figure.

If the polygon vertices are \(p_1, p_2, \ldots, p_n\) then we need to check that

\begin{equation*} sorient(P, p_1, p_2) = sorient(P, p_2, p_3) = \ldots = sorient(P, p_{n - 1}, p_n) = sorient(P, p_n, p_1) \end{equation*}

Paste this command into your terminal:

The password to connect is

Point in convex polygon

You are given a convex polygon and a set of points. For each given point, check whether it lies inside the polygon, outside of it or on its the boundary.

Note: This problem is not about making a smart data structure to efficiently answer the queries. Checking the above condition in linear time is sufficient.

Input

One line with one integer \(n\) giving the number of vertices of the polygon.
\(n\) lines each with two integers \(x_i\) and \(y_i\) giving the coordinates of the polygon vertices.
One line with one integer \(q\) giving the number of query points.
\(q\) lines each with two integers \(X_i\) and \(Y_i\) giving the coordinates of the query points.

We guarantee that the input polygon is simple and convex.

Output

\(q\) lines, one for each query. If point \((X_i, Y_i)\) lines inside the polygon, the \(i\)-th line should contain the word inside. If it lies outside, it should contain outside. Otherwise print boundary.

Constraints