Geometry - Point orientation - Competitive Programming

Geometry - Point orientation

One of the main uses of cross product is in determining the relative position of points and other objects. For this, we define the function $orient(A, B, C) = \vec{AB} \times \vec{AC}$ . It is positive if $C$ is on the left side of $\vec{AB}$ , negative on the right side, and zero if $C$ is on the line containing $\vec{AB}$ .

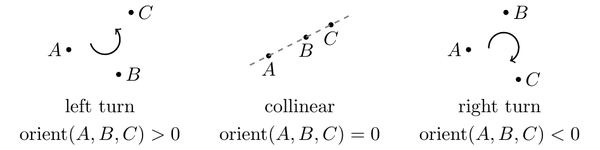
It is straightforward to implement:

// create the vector from point a to point b
static Point vec(Point a, Point b) {
    return new Point(b.x - a.x, b.y - a.y);
}

static double orient(Point a, Point b, Point c) {
    return cross(vec(a, b), vec(a, c));
}

In most situations we only care about the sign of $orient(a, b, c)$ . Therefore we define a function $sorient(a, b, c)$ which returns the sign of $orient(a, b, c)$

$\begin{equation*} sorient(a, b, c) = \begin{cases} 1 & \quad orient(a, b, c) > 0 \\ 0 & \quad orient(a, b, c) = 0 \\ -1 & \quad orient(a, b, c) < 0 \end{cases} \end{equation*}$

static double sorient(Point a, Point b, Point c) {
    double o = orient(a, b, c);
    return o < 0 ? -1 : o > 0 ? 1 : 0;
}

Paste this command into your terminal:

The password to connect is

Point in angle

As an example of use of the orientation of three points, write an function to check whether a point $P$ lies strictly inside the angle formed by two semi-lines $AB$ and $AC$ .

For instance, in the following figure, in the first two cases the point $P$ does not lie inside the angle and in the last case it does.