Geometry - 2D Rotation - Competitive Programming

Geometry - 2D Rotation

Imagine you have a point $p$ which you want to rotate at an angle $\theta$ around a point $c$ as shown in the following figure.

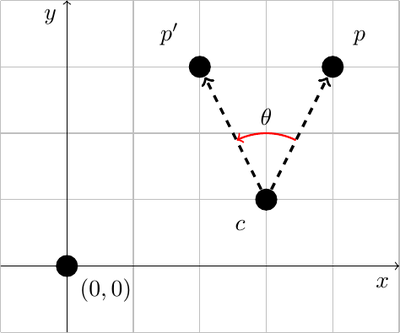
The first step is to know how to rotate a point around the origin because when you know how to do that, you will be able to rotate a point $p$ around another point $c$ in the new coordinate system whose origin is $c$.

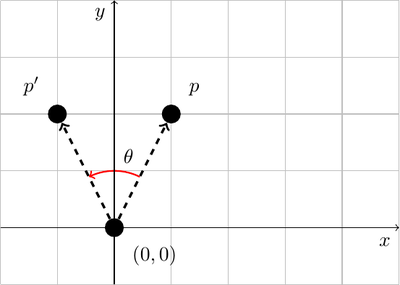
In 2D, we can define the point $p'$, the point p rotated around the origin by an angle $\theta$ ($\theta$ measured counter-clockwise) as follows :

\begin{align*} p'_x = p_x \cdot \cos \theta - p_y \cdot \sin \theta\\ p'_y = p_x \cdot \sin \theta + p_y \cdot \cos \theta \end{align*}

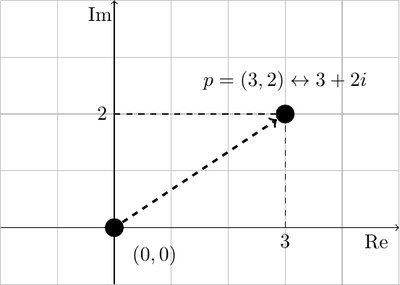
To see why this is the case, we will reason about $p$ and $p'$ as complex numbers. There is a natural one to one correspondence between the 2D plane and the set of complex numbers. A point $p = (x, y)$ corresponds to the complex number $x + i y$.

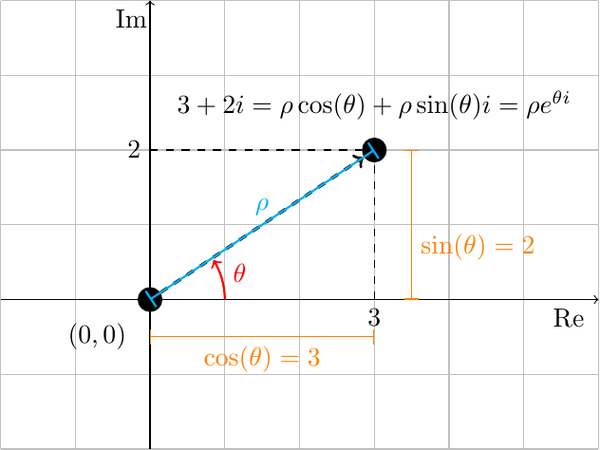
We know that complex number can be expressed as $x + i y = \rho e^{i \theta}$ where $\rho$ is the distance to the origin and $\theta$ is the angle between the x-axis and the segment connecting the origin to point $(x, y)$.

The reason why this expression is useful is that multiplications behaves as expected, that is,

\begin{equation*} \rho_1 e^{i \theta_1} \cdot \rho_2 e^{i \theta_2} = \rho_1 \cdot \rho_2 e^{i \cdot (\theta_1 + \theta_2)} \end{equation*}

This means that the result of multiplying two complex numbers is a complex number whose distance to the origin is the product of the distances of the two input numbers and the angle is the addition. This is show in the following figure.

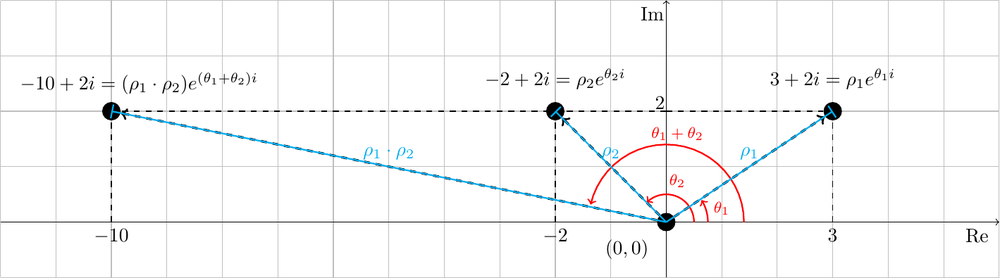
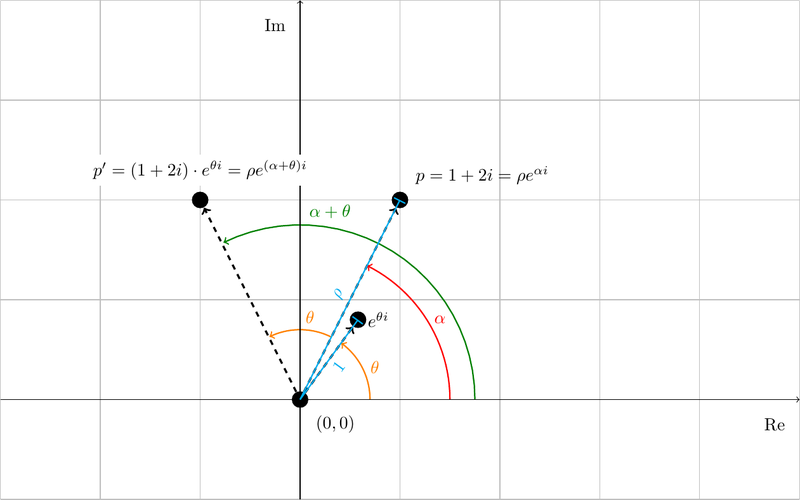
Therefore, in particular, to rotate a point $(x, y)$ of an angle $\theta$ around the origin we simply need to multiply the complex number $x + i y$ by $e^{i \theta}$. The reason why this works is that if we write $x + i y = \rho e^{i \alpha}$ for some $\rho$ and $\alpha$ then

\begin{equation*} (x + i y) \cdot e^{i\theta} = \rho e^{i \alpha} \cdot e^{i \theta} = \rho e^{i (\alpha + \theta)} \end{equation*}

Which is exacly the same point except that we added $\theta$ to the angle. The next figure illustrates this.

Finally, to deduce the above formulas for the roation we simply need to compute the expression of $x' + iy' = (x + i y) \cdot e^{i\theta}$ by remembering that $e^{i\theta} = \cos \theta + i \sin \theta$. and $i^2 = -1$:

\begin{equation*} \begin{split} (x + yi)\cdot e^{i\theta} & = (x + yi)\cdot (\cos \theta + i \sin \theta)\\ & = x\cdot \cos \theta + x \cdot i \cdot \sin \theta + y \cdot i \cdot \cos \theta - y \cdot \sin \theta \\ & = (x\cdot \cos \theta - y\cdot \sin \theta) + i\ (x\cdot \sin \theta + y\cdot \cos \theta) \end{split} \end{equation*}

So that

\begin{align*} x' = x \cdot \cos \theta - y \cdot \sin \theta\\ y' = x \cdot \sin \theta + y \cdot \cos \theta \end{align*}

To rotate a point p around another point c, we need to rotate the point p expressed in the coordinate system whose origin is c (it simply is $p-c$), and then we just need to express the result in the initial coordinate system (whose origin is (0,0)).

This gives us the following formula (if we define $p' = p'_x + p'_yi$):

\begin{equation*} p' = c + e^{i \theta} \cdot (p - c) \end{equation*}

or :

\begin{align*} p'_x = c_x + (p_x - c_x) \cdot \cos \theta - (p_y - c_y) \cdot \sin \theta\\ p'_y = c_y + (p_x - c_x) \cdot \sin \theta + (p_y - c_y) \cdot \cos \theta \end{align*}

Note : similar computations (with a different result) could be done for an angle measured clockwise. In fact, we would just have to change $\theta$ into $-\theta$.

In Java, we can easily implement these functions as follows.

static Point rotate(Point p, double a) {
    return new Point(p.x * Math.cos(a) - p.y * Math.sin(a), p.x * Math.sin(a) + p.y * Math.cos(a));
}

static Point rotate(Point p, Point c, double a) {
    return new Point(c.x + (p.x - c.x) * Math.cos(a) - (p.y - c.y) * Math.sin(a),
                   c.y + (p.x - c.x) * Math.sin(a) + (p.y - c.y) * Math.cos(a));
}

Paste this command into your terminal:

The password to connect is

Object rotating

As an exercise, compute the result of rotating an object by a certain angle $\theta$ around a center $c$.

Input

One line with an integer $n$ giving the number of vertices of the object.
One line with an integer $\theta$ giving the counter-clockwise angle for the rotation (in degrees).
One line with two integers $c_x$ and $c_y$ giving the coordinates of the center of rotation.
$n$ lines with two integers $x_i$ and $y_i$ giving the coordinates of the object vertices.

Constraints

$1 \leq n \leq 1000$
$0 \leq \theta \leq 1080$
$-1000 \leq c_x, c_y \leq 1000$
$-1000 \leq x_i, y_i \leq 1000$

Output

$n$ lines, each giving the two coordinates of one of the points of the rotated object. These points must be in the same order as the ones given in the input. The two coordinates must be separated by a single space.

The will be accepted as long as it is accurate up to $10^{-6}$ relative or absolute precision.

Sample Test Cases

Max file size: 1.0 MiB
Allowed extensions: .java, .cpp, .py

Author(s)	Alexandre Gobeaux, Victor Lecomte, François Aubry
Deadline	No deadline
Submission limit	No limitation

Information

Sign in