The cross product $\vec{v} \times \vec{w}$ of two vectors $\vec{v}$ and $\vec{w}$ can be seen as a measure of how perpendicular they are.

It is defined in 2D as:

where $\|\vec{v}\|$ and $\|\vec{w}\|$ are the lengths of the vectors and $\theta$ is the amplitude of the oriented angle from $\vec{v}$ to $\vec{w}$.

The cross product has a very simple expression in cartesian coordiantes. If $\vec{v} = (v_x, v_y)$ and $\vec{w} = (w_x, w_y)$ then

static double cross(Point v, Point w) {
    return v.x * w.y - v.y * w.x;
}

Geometric interpretation

The cross product $\vec{v} \times \vec{w}$ can be seen as a measure of how perpendicular the two vectors are.

The sign of the cross product indicates whether $\vec{w}$ is to the left or to the right of $\vec{v}$.

• $\vec{v} \times \vec{w} > 0$: $\vec{w}$ is to the left of $\vec{v}$
• $\vec{v} \times \vec{w} < 0$: $\vec{w}$ is to the right of $\vec{v}$
• $\vec{v} \times \vec{w} = 0$: $\vec{w}$ and $\vec{v}$ are aligned

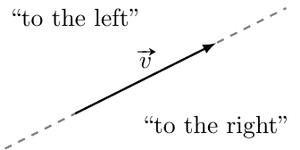
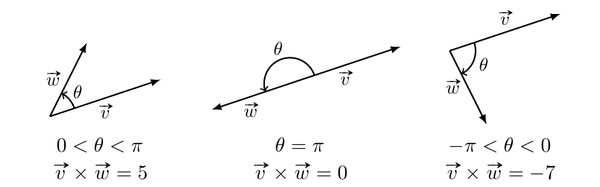
In general, we take the angle between the vectors $\theta$ in $]-\pi, \pi]$ so that the dot product is positive if $0 < \theta < \pi$, negative if $-\pi < \theta < 0$ and zero if $\theta = 0$ or $\theta = \pi$: