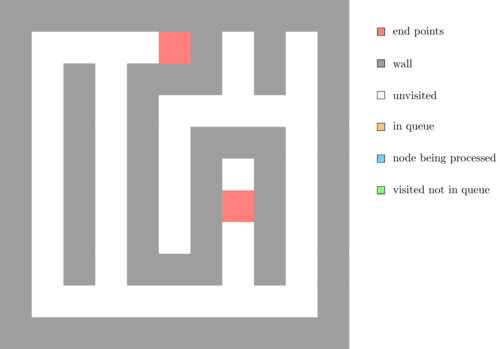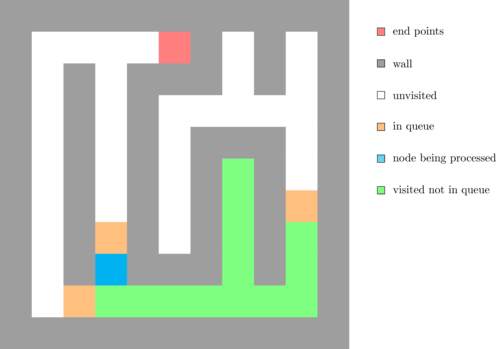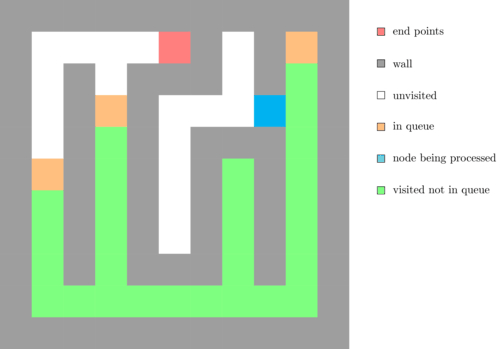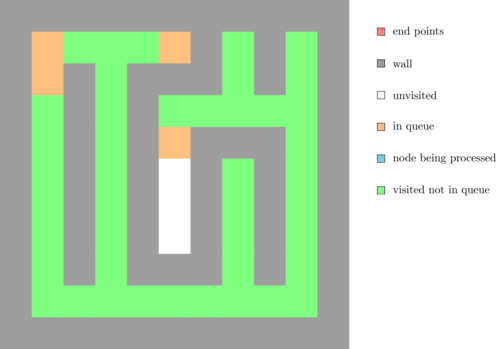
We are now going to see how we can solve mazes as the one show below. The goal is to find a path in the maze connecting the two blue points.

We can simply use the path finding algorithm implemented before. What we are going to learn here is to avoid representing the graph explicitly and execute the path finding algorithm directly on the maze.
It is easy to represent the maze problem as a pathfinding problem on a graph. The graph has one node for each white cell in the maze. There is an edge between two nodes if the corresponding white cells are adjacent. The following figure illustrates this.
Example:
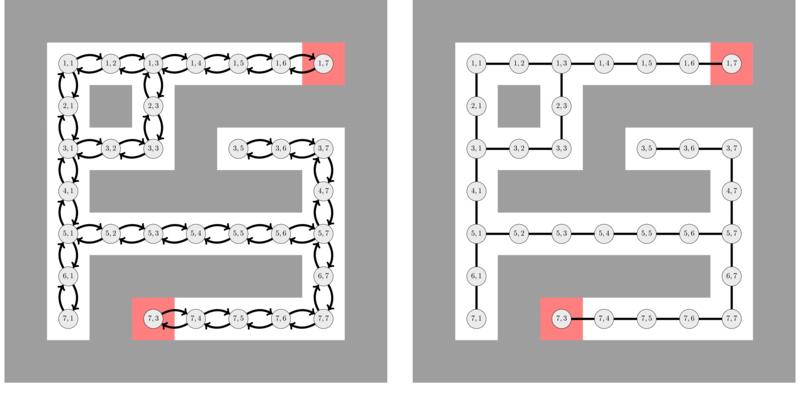
Notice that in this case graph, whenever there is an edge \((u, v)\) the reversed edge \((v, u)\) also exists. This is because if we can go from cell \(x\) to cell \(y\) we can also move from cell \(y\) to cell \(x\). In this case we say that the graph is undirected. Usually edges in undirected graphs are represented by segments as shown in the right figure instead of having the two arrows. From now on this will be how we represent undirected graphs graphically.
One way to solve this problem is to explicitly build the graph that corresponds to the maze and call findPath. However we will not do this. Instead we will re-implement the algorithm to run over the maze without explicitly building the graph.
We represent the maze as an ASCII matrix \(maze\) using '# for the walls, '.' for the white space, 'S' for the starting point and 'T' for the destination.
Example:
The above maze will be represented by:
#########
#......S#
#.#.#####
#...#...#
#.#####.#
#.......#
#.#####.#
#.#T....#
#########
Nodes will be represented with array of two elements. So node \(u = (i, j)\) is represented in code as int[] u = new int[] {i, j}.
When we are at node \((i, j)\) we know that our candidate neighbors are:
From these we need to remove the ones that correspond to a wall. To easily iterate over them it is convenient to declare an array with the possible movement directions:
static int[][] dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
Then to iterate over the neighbours of \(u = [u_i, u_j]\) we can simply do:
for(int[] d : dir) {
int i = u[0] + d[0];
int j = u[1] + d[1];
if(maze[i][j] != '#') {
// do something, the neighbour (i, j) of u
}
}
Putting these pieces together to make a pathfinding algorithm is straightforward. As before, we need to be able to mark a node as visited. The simplest way to do this with when nodes are pairs of integers is to create a matrix such that \(visited[i][j]\) is true if and only if node \((i, j)\) has been visited. Another change is that the parent will also be stored in an array such that \(parent[i][j]\) contains the parent of node \((i, j)\).
static ArrayList<int[]> findPath(int n, int m, char[][] maze, int[] start, int[] end) {
// initialize the queue and visited matrix
Queue<int[]> Q = new LinkedList<>();
Q.add(start);
boolean[][] visited = new boolean[n][m];
// initialize the parent array
int[][][] parent = new int[n][m][];
visited[start[0]][start[1]] = true;
// in practice you might want to stop as soon as end is visited
while(!Q.isEmpty()) {
int[] u = Q.poll();
// we are now processing node u
for(int[] d : dir) {
int i = u[0] + d[0];
int j = u[1] + d[1];
// visit the edge from u to (i, j)
if(!visited[i][j] && maze[i][j] == '.') {
// node (i, j) has not yet been visited and is not a wall, add it
Q.add(new int[] {i, j});
visited[i][j] = true;
// set the parent of (i, j) to be u
parent[i][j] = u;
}
}
}
// check whether a path exists
if(!visited[end[0]][end[1]]) return null;
// build the path by tracing back from t to s
ArrayList<int[]> path = new ArrayList<>();
int[] cur = end;
// loop until we reach s (s is the only visited node with null parent)
while(parent[cur[0]][cur[1]] != null) {
path.add(cur);
cur = parent[cur[0]][cur[1]];
}
// reverse and return the path
Collections.reverse(path);
return path;
}
The following animation illustrates an execution of this algorithm.
 INGInious
INGInious