An undirected graph is said to be bipartite if its nodes can be partitioned into two disjoint sets \(L, R\) such that there are no edges between any two nodes in the same set.
Example:
Consider the following graph.
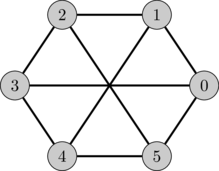
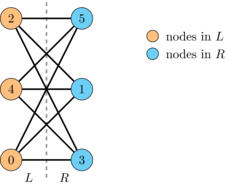
This is a bipartite graph because if we set \(L = \{0, 2, 4\}\) and \(R=\{1,3,5\}\) then there are no edges between any two nodes in \(L\) nor \(R\). To better see this, we can draw the graph again by putting the nodes in \(L\) on the left and the nodes in \(R\) on the right.
Checking whether an undirected graph is bipartite graph should be an easy task by adapting the BFS code. We encourage you to try to write you own algorithm to do so.
It can also be computed using the distance array. Just compute the distance labels on each connected component, starting at any node on the left for each of them. Then loop over the edges and check whether every edge links a node with even distance to a node with odd distance. The graph will be bipartite if and only if this holds.
The reason why this works is that paths starting on \(L\) on a bipartite graph must alternate between \(L\) and \(R\). Thus, as there are no edges within the sets, the distances must also alternate between even and odd from one side to the other. The first node will be even (distance 0) on the left then its neighbors will be odd (distance 1) on the right, then the neighbors of the neighbors will be even (distance 2) on the left and so on.
The following animation illustrates this.
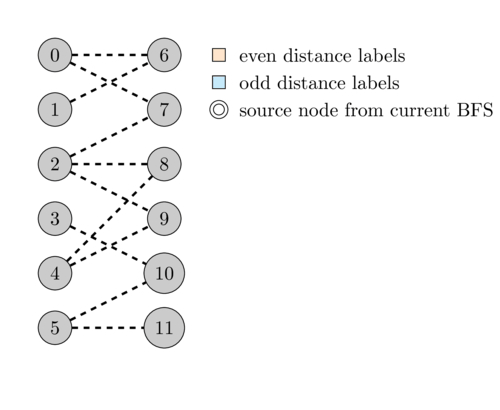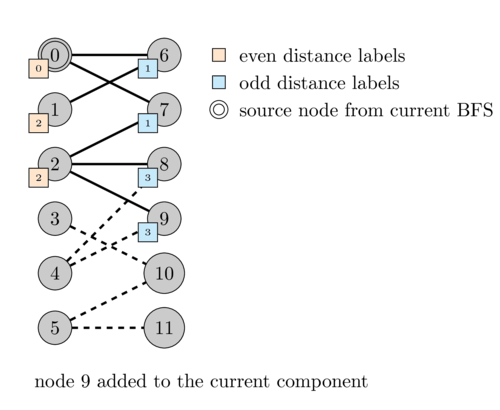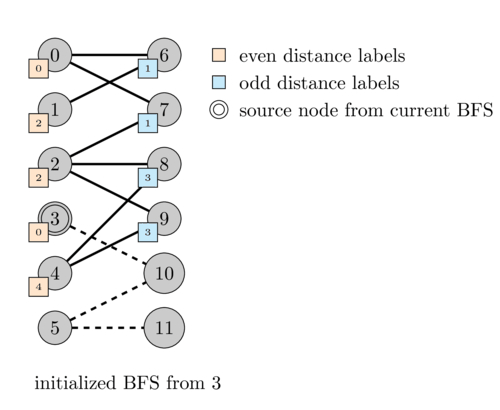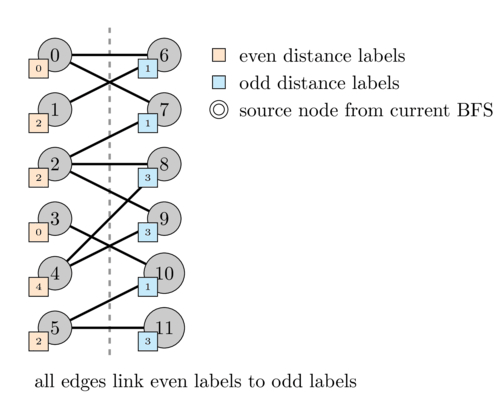
One can observe that a graph is bipartite if and only if it does not contain a cycle of odd length. This is because we saw that any path must alternate between even and odd distances. Thus, since a cycle starts and ends at the same node, it would mean that some node in the cycle is both labeled as even and odd which is impossible.
This is an important result that we will use later. It also means that now we have a simple way to check whether a graph contains cycles of odd length.
 INGInious
INGInious