Suppose that you have a set of \(n\) tasks to perform some of which depend on each other. If a task \(t\) depends on taks \(t_1, t_2, \ldots, t_k\) then we can only do task \(t\) after having done all the tasks \(t_1, t_2, \ldots, t_k\). We would like to compute an order in which we can perform the tasks.

The tasks and precedences are naturally modeled by a graph with one node per task and an edge from task \(t_i\) to \(t_j\) if and only if task \(t_j\) depends on task \(t_i\).

Example:

Consider the simple example of getting dressed. There are some clothing items that you cannot put before others. For instance, the undershorts must be put before the pants, the socks before the shoes and so on.

The following image shows a graph on the top with a possible list of precedences for some items of clothing.

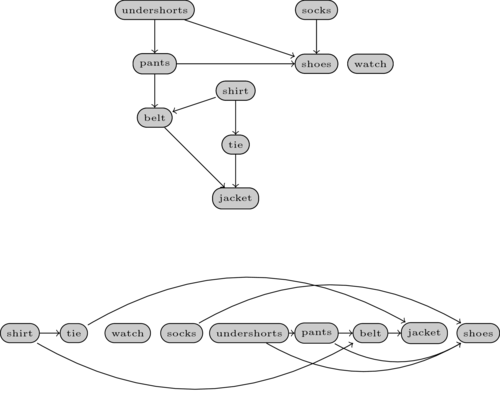
The graph on the bottom shows a possible order. We draw the edges to make it clear that all of them go from the left to the right, meaning that no precedences are violated.

We define the in-degree of a node \(u\) as the number of edges that end in \(u\) and the out-degree as the number of edges that start at it. They are denoted by \(indeg(u)\) and \(outdeg(u)\), respectively.

It is easy to see that any topological order must start with a node with in-degree \(0\) since such a node has no precedences. Then, if we remove that node from the graph the same is true from the resulting graph: the next node can by any node with in-degree \(0\). This suggests the following algorithm.

Compute the in-degree of each node. Put all the nodes with in-degree \(0\) in a queue to be processed. While there are nodes to be processed: select one to process, add it in the next position in the order and delete it by decreasing the in-degree of all of its sucessors while adding new nodes with in-degree \(0\) to the queue.

The following animation illustrates an execution of this algorithm on the sample graph given above.

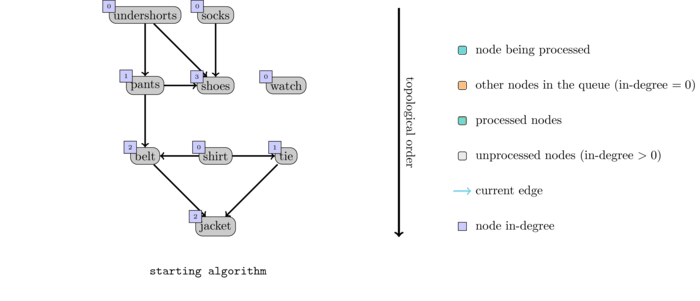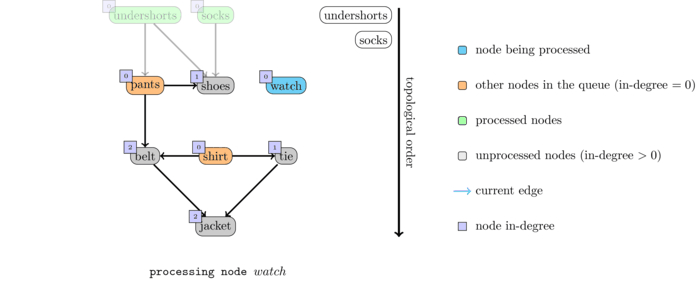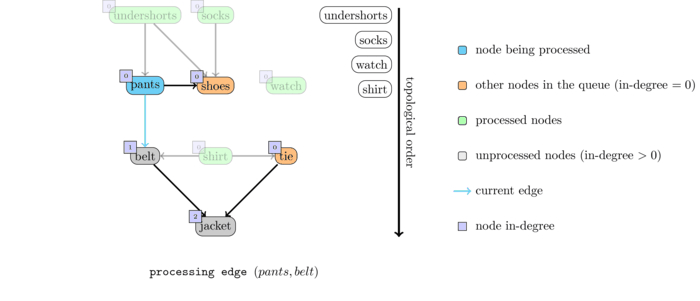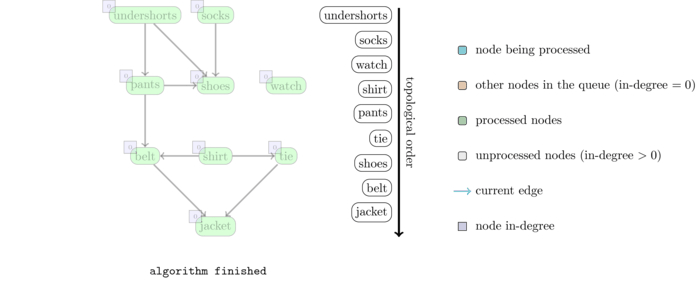
If you think about it, this algorithm is quite similar to the BFS. The differences are:

1. We start from multiple points (all nodes with in-degree \(0\) ), not a single source.
2. We only add a node when its in-degree becomes \(0\).

As you can see, the code is quite similar:

static ArrayList<Integer> toposort(LinkedList<Integer>[] g) {
    // compute the in-degrees
    int[] indeg = new int[g.length];
    for(int u = 0; u < g.length; u++) {
        for(int v : g[u]) {
            indeg[v] += 1;
        }
    }
    // initialize the queue with 0 in-degree nodes
    Queue<Integer> Q = new LinkedList<>();
    for(int u = 0; u < g.length; u++) {
        if(indeg[u] == 0) {
            Q.add(u);
        }
    }
    ArrayList<Integer> order = new ArrayList<>();
    while(!Q.isEmpty()) {
        int u = Q.poll();
        // add u as the next node in the topological order
        order.add(u);
        // we are now processing node u
        for(int v : g[u]) {
            // visit edge (u, v)
            indeg[v] -= 1;
            if(indeg[v] == 0) {
                // node v has now in-degree 0, add it to the queue
                Q.add(v);
            }
        }
    }
    return order;
}

Note: This algorithm assumes that the input graph is acyclic and that the topological order exists. If there are cycles in the graph then the nodes in those cycles will have a positive degree at the end of the execution. Thus you can check whether the order is valid by checking if some node has a positive degree at the end of the execution. Note however that it is not true that in the presence of cycles only nodes in cycles can have a positive degree in the end. Thus you cannot use this criteria to output all nodes that belong to a cycle.

Example:

The following animation shows an execution of the algorithm on a graph that contains cycles.

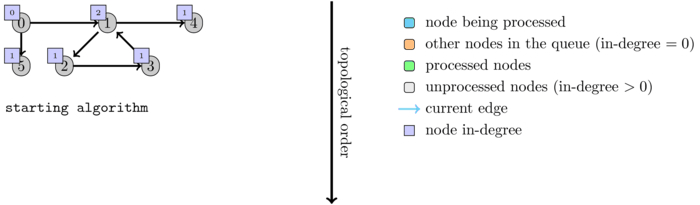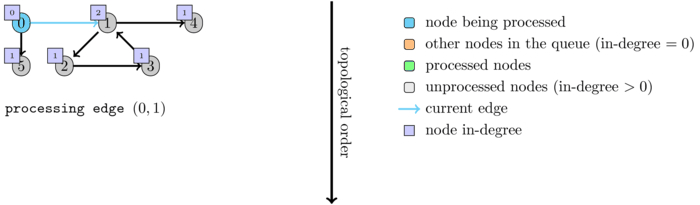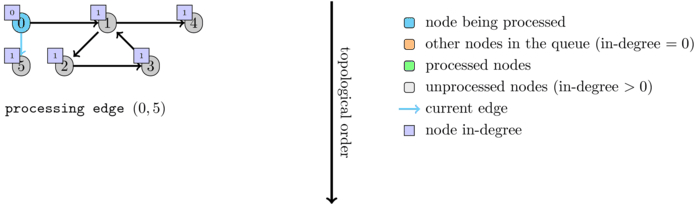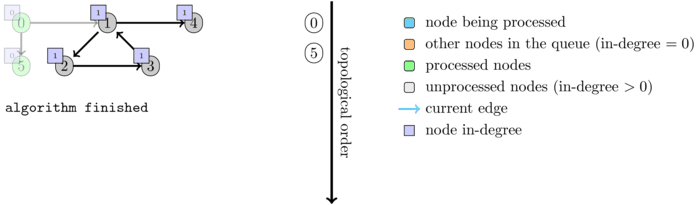
Another way to see if the order exists (for an acyclic graph) is simply to see whether the size of \(order\) is equal to the number of nodes.