0. Assignment Instructions
Before starting with your Java implementation, read the assignment instructions and grading rules on the course web page: https://user.it.uu.se/~pierref/courses/COCP/assignments/assignment5/assignment5.pdf .
This part of the assignment is on the programming tasks of Modules 3 to 5 of the MiniCP on-line teaching materials.
In the programming part of this assignment, you will implement:
- The
Element1Dconstraint; - The
Element1DDCTestconstraint; - The
Element1DVarconstraint; - The
StateSparseBitSetdata structure and theTableCTconstraint; - The
AllDifferentFWCconstraint using basic forward checking filtering; and - The
AllDifferentDCconstraint using an advanced and efficient domain constistent filtering;
The data structure and constraints can then be used to model the Stable Matching and Eternity problems.
1. Element1D Constraint - Bound-Consistent Propagator
Given an array T of integers and the variables y and z, the Element1D constraint enforces that z takes the value at index
y of T: the relation T[y]=z must hold, where indexing starts from 0.
Assuming T=[1,3,5,7,3], the constraint holds for
y = 1, z = 3 y = 3, z = 7
but is violated for
y = 1, z = 1 y = 3, z = 5
Implement a propagator
Element1D.java
by following the ideas (also in the slides) for Element2D,
which lead to bound consistency on z and domain consistency on y.
Check that your implementation passes the tests
Element1DTest.java.
2. Element1D Constraint - Domain-Consistent Propagator
Now that you have implemented a bound-consistent propagator for the Element1D constraint, you can implement another one for the same constraint, reaching domain consistency.
Within Element1DDomainConsistent.java, implement a propagator that achieves domain consistency for both variables.
One way to implement the domain-consistent version is to check if the constraint holds for every value within the domain of y and z. To iterate over their domains, you can use your efficient IntVar.fillArray that you implemented previously:
int size = y.fillArray(values);
for (int i = 0 ; i < size ; i++) {
int valueOfY = values[i];
// check if valueOfY (one element from the domain of y) is valid. Remove it otherwise
}
Keep in mind that values should be a container array stored as an instance variable from Element1DDomainConsistent and reused many times.
It is important for efficiency to avoid creating objects on the heap at each execution of a propagator.
Never forget that a propagate() method of Constraint may be called thousands of times per second.
Check that your implementation passes the tests Element1DDCTest.java.
3. Element1DVar Constraint with an Array of Variables
Implement a propagator
Element1DVar.java.
This constraint is more general than Element1D above,
since T is here an array of variables.
The filtering algorithm is nontrivial, at least if you want to do it efficiently. Two directions of implementation are:
- The hybrid domain-bound consistent propagator
achieves bound consistency for
zand all theT[i]but domain consistency fory. - The domain-consistent propagator
achieves domain consistency for
y,z, and all theT[i].
Check that your implementation passes the tests Element1DVarTest.java. Those tests do not check that your propagator achieves domain consistency for all the variables, so you have to write additional tests in order to help convince yourself that it does so, if you take that direction.
4. Table Constraint
a. Implementing the Residues
Fill in all the gaps of the StateSparseBitSet data structure in order to add the concept of residue (the idea of caching the last word with a non-empty intersection) so as to have an efficient algorithm.
Your task is to finish the implementation in StateSparseBitSet.java:
- Implement the check of the intersection for the word remembered by the residue (TODO 1).
- Implement the update of the residue (TODO 2).
Check that your implementation passes the tests StateSparseBitSetTest.java.
b. Compact-Table
Fill in all the gaps of the Compact-Table algorithm. This implementation uses StateSparseBitSet and maintains the state (the set of valid tuples) from one propagation to another. You will need to have completed the previous question before beginning this implementation.
Your task is to finish the implementation in TableCT.java:
- Add the filling of the supports StateSparseBitSets (TODO 1). You can test that your filling is correct by running the tests
testInitSupports1andtestInitSupports2from TableCTTest.java. - Implement the
hasChangedmethod (TODO 2). It is the heart of the incremental updates: it must returntrueif the domain size of a variable has changed since the last propagation. - Within the propagation function, implement the computation of the set of supported tuples (TODO 3). You can test that the computation is done correctly by running the tests
testSetSupportedTuples1andtestSetSupportedTuples2. - Within the propagation function, implement the condition for removing a given value (TODO 4)
For the filling of the supports (TODO 1), look at the following table, composed of one column:
| Index | \(X\) |
|---|---|
| 0 | 5 |
| 1 | 2 |
| 2 | 4 |
| 3 | 1 |
| 4 | 0 |
| 5 | 2 |
Assume that \(D(X)={0,2,4}\). Then the supports of \(X\) when initializing the Table constraint are the following (only the last 6 bits are shown):
support(X, 0):010000- row 4 is validsupport(X, 1):000000- no valid rowsupport(X, 2):100010- rows 1 and 5 are both validsupport(X, 3):000000- no valid rowsupport(X, 4):000100- row 2 is valid
Your fully implemented class should pass all the tests from TableCTTest.java.
5. AllDifferent Forward-Checking Filtering
Implement a dedicated propagator AllDifferentFWC.java
for the global AllDifferent constraint.
Unlike AllDifferentBinary.java,
it must not decompose the AllDifferent constraint by posting binary disequality
constraints but instead do the following: when a variable becomes fixed, its value is removed from the domains of all the other variables.
This achieves the same filtering as AllDifferentBinary.java, namely what is called forward-checking consistency. Avoid iteration over already fixed variables when removing a value: implement the sparse-set technique, as done in Sum.java.
Test your implementation in AllDifferentFWCTest.java.
6. AllDifferent Domain-Consistent Filtering
Now that the basic algorithm is completed, let's implement an effective one! You will implement the filtering algorithm described in [Regin94]
to remove every impossible value for the AllDifferent constraint (this is called generalized arc consistency and is also known as domain consistency).
More precisely, you must:
- Implement the constraint AllDifferentDC.java.
- Test your implementation in AllDifferentDCTest.java.
Régin's algorithm is a four-step procedure that can be described with the following figure:
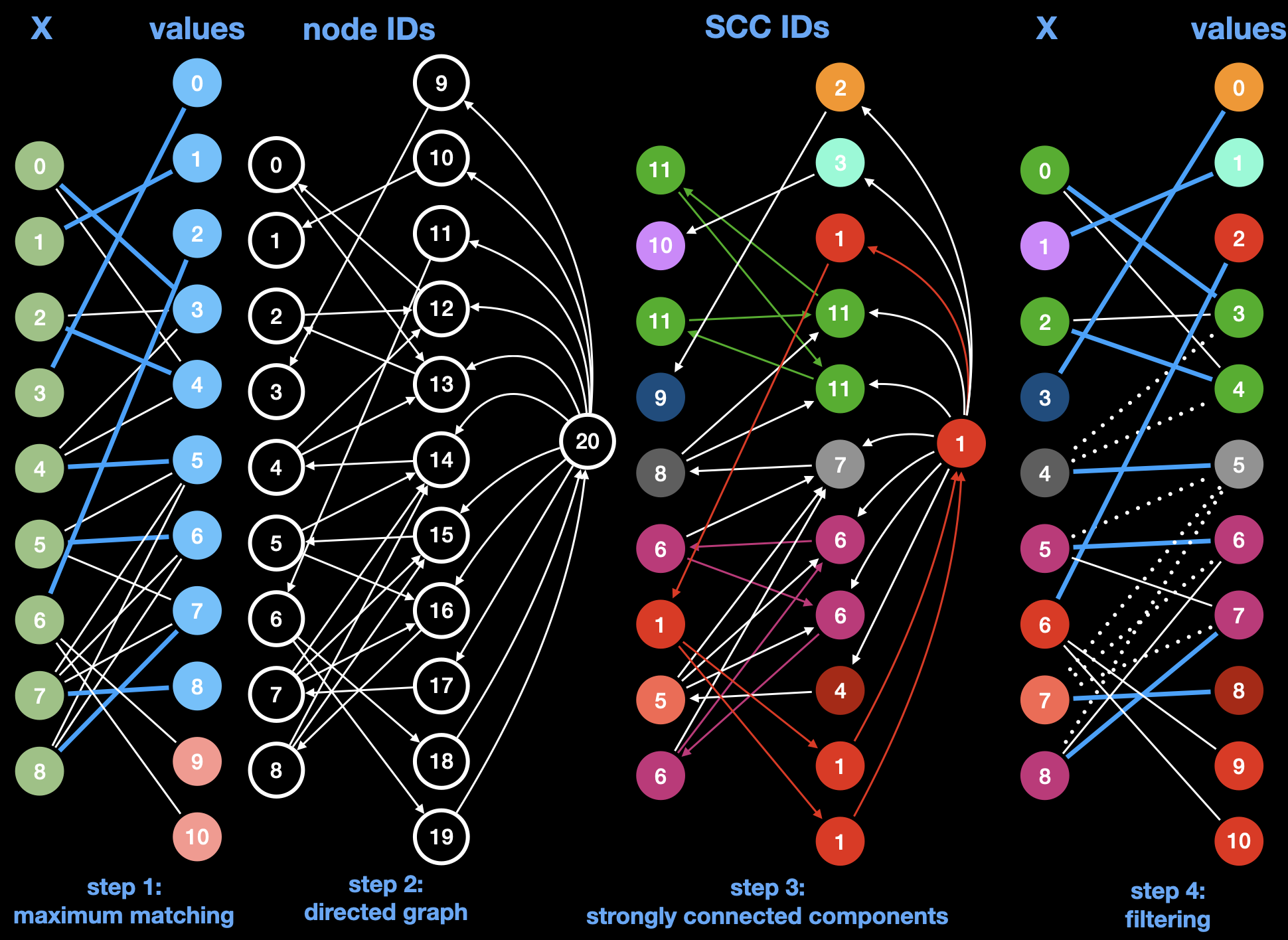
The four steps are:
- Compute an initial maximum matching in the variable-value graph for the feasibility test (matched edges and value nodes are colored blue in the figure).
- Build a directed graph: each matched edge becomes a directed arc to the variable node from the
value node, and each unmatched edge becomes a directed arc to the value node from the
variable node. Additionally, a dummy node is added
that has an incoming arc from each unmatched value node, and an outgoing arc to each matched value node.
You can test that your graph is correctly built by running the tests
testUpdateGraph1,testUpdateGraph2andtestUpdateGraph3. You need to call theupdateGraphmethod within thepropagatefor the tests to work. - Compute the strongly connected components (SCCs). Note that, for this step, the number of each node in the figure corresponds to their SCC rather than their index or value for variable and value nodes respectively.
- Remove every arc that was not a matched edge and that connects two nodes from different components is. Note that, for this step, the number of each node in the figure once again corresponds to their index or value for variable and value nodes respectively.
The two main algorithmic building blocks are provided:
- MaximumMatching.java
is a class that computes a maximum matching given an array of variables.
You should use its
computemethod in thepropagatemethod. - GraphUtil.java
contains a static method with signature
public static int[] stronglyConnectedComponents(Graph graph)to compute the strongly connected components. The returned array gives for each node its SCC identifier.
One of the main difficulties of this exercise is to implement the Graph interface
to represent the residual graph of the maximum matching:
public static interface Graph {
/* the number of nodes in this graph */
int n();
/* incoming nodes ids incident to node idx */
Iterable<Integer> in(int idx);
/* outgoing nodes ids incident to node idx */
Iterable<Integer> out(int idx);
}
It uses an adjacency list that is updated in the method updateGraph().
We advise you to use a dense representation with node ids as illustrated on the black nodes of the figure (step2: directed graph).
7. Comparing the Two AllDifferent Filtering Algorithms
Once your code passes the tests, you can experiment your new filtering on the N-Queens model in order to see the improvements. Improvements can come in one of the following ways:
- Is the search tree smaller when using the domain-consistent filtering?
- Is the model faster?
Your new N-Queens model might not include both ways of improvement, but it certainly has at least one of them.
| [Regin94] | Régin, J.-C. (1994). A filtering algorithm for constraints of difference in CSPs. 12th National Conference on Artificial Intelligence (AAAI-94). (PDF) |
Before submitting, remember to fetch the latest changes from upstream (the MiniCP GitHub repository).
Note that the original tests of the MiniCP GitHub repository will be run.
 INGInious
INGInious