1. Forward-Checking Filtering

Implement a dedicated propagator AllDifferentFWC.java for the global AllDifferent constraint. Unlike AllDifferentBinary.java, it must not decompose the AllDifferent constraint by posting binary disequality constraints but instead do the following: when a variable becomes fixed, its value is removed from the domains of all the other variables.

This achieves the same filtering as AllDifferentBinary.java, namely what is called forward-checking consistency. Avoid iteration over already fixed variables when removing a value: implement the sparse-set technique, as done in Sum.java.

Test your implementation in AllDifferentFWCTest.java. Modify NQueens.java by using AllDifferentFWC.java and experiment with the 15-queens instance: how much speed-up do you observe for finding all the solutions?

2. Domain-Consistent Filtering

Now that the basic algorithm is completed, let's implement an effective one! You will implement the filtering algorithm described in [Regin94] to remove every impossible value for the AllDifferent constraint (this is called generalized arc consistency and is also known as domain consistency). More precisely, you must:

• Implement the constraint AllDifferentDC.java.
• Test your implementation in AllDifferentDCTest.java.

Régin's algorithm is a four-step procedure that can be described with the following figure:

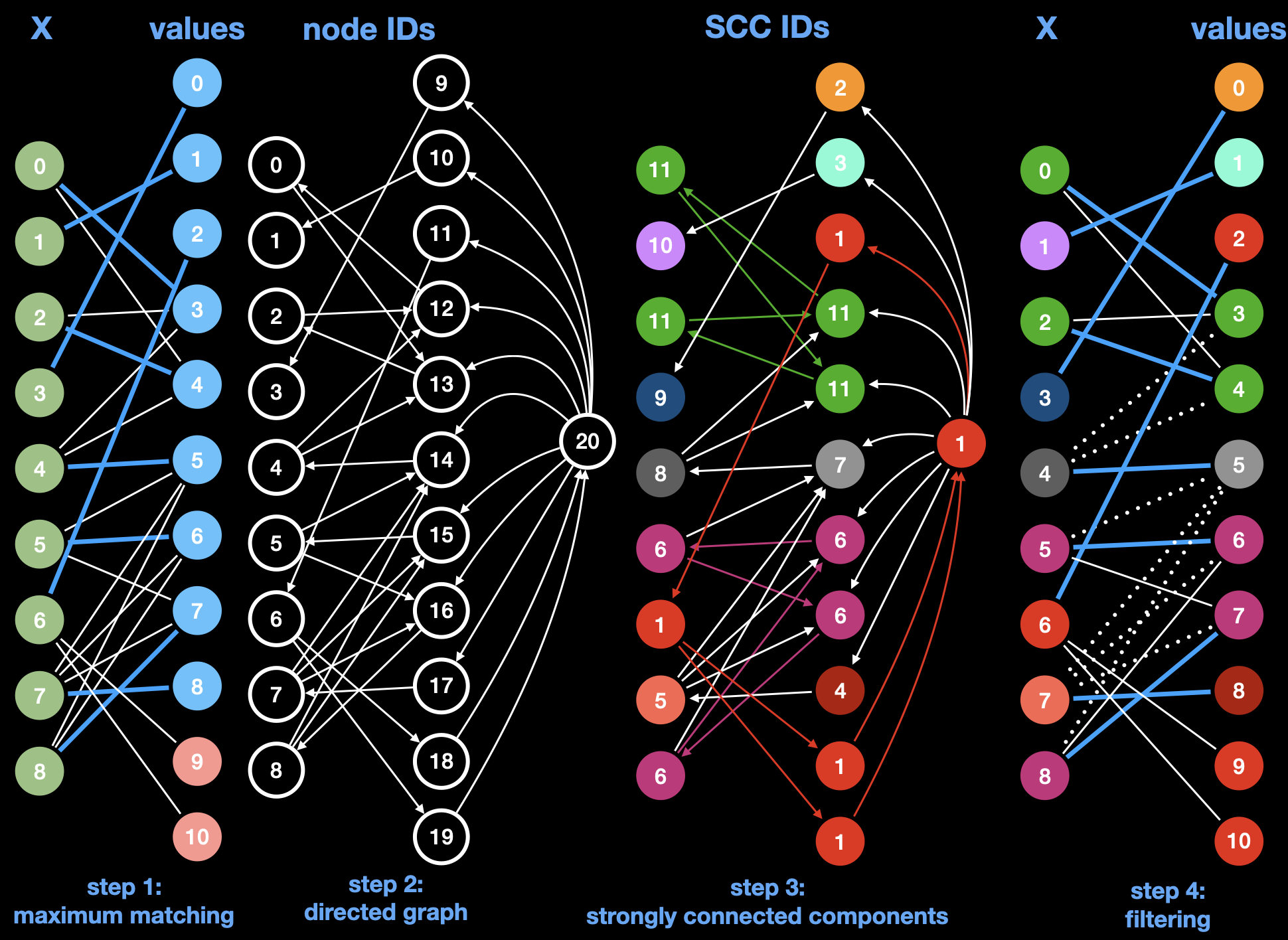
The four steps are:

1. Compute an initial maximum matching in the variable-value graph for the feasibility test (matched edges and value nodes are colored blue in the figure).
2. Build a directed graph: each matched edge becomes a directed arc to the variable node from the value node, and each unmatched edge becomes a directed arc to the value node from the variable node. Additionally, a dummy node is added that has an incoming arc from each unmatched value node, and an outgoing arc to each matched value node. You can test that your graph is correctly built by running the tests testUpdateGraph1, testUpdateGraph2 and testUpdateGraph3. You need to call the updateGraph method within the propagate for the tests to work.
3. Compute the strongly connected components (SCCs). Note that, for this step, the number of each node in the figure corresponds to their SCC rather than their index or value for variable and value nodes respectively.
4. Remove every arc that was not a matched edge and that connects two nodes from different components is. Note that, for this step, the number of each node in the figure once again corresponds to their index or value for variable and value nodes respectively.

The two main algorithmic building blocks are provided:

• MaximumMatching.java is a class that computes a maximum matching given an array of variables. You should use its compute method in the propagate method.
• GraphUtil.java contains a static method with signature public static int[] stronglyConnectedComponents(Graph graph) to compute the strongly connected components. The returned array gives for each node its SCC identifier.

One of the main difficulties of this exercise is to implement the Graph interface to represent the residual graph of the maximum matching:

public static interface Graph {
    /* the number of nodes in this graph */
    int n();

    /* incoming nodes ids incident to node idx */
    Iterable<Integer> in(int idx);

    /* outgoing nodes ids incident to node idx */
    Iterable<Integer> out(int idx);
}

It uses an adjacency list that is updated in the method updateGraph(). We advise you to use a dense representation with node ids as illustrated on the black nodes of the figure (step2: directed graph).

3. Comparing the Two Filtering Algorithms

Once your code passes the tests, you can experiment your new filtering on the N-Queens model in order to see the improvements. Improvements can come in one of the following ways:

• Is the search tree smaller when using the domain-consistent filtering?
• Is the model faster?

Your new N-Queens model might not include both ways of improvement, but it certainly has at least one of them.