INGIniousOn considère dans le plan la région
\begin{equation*}
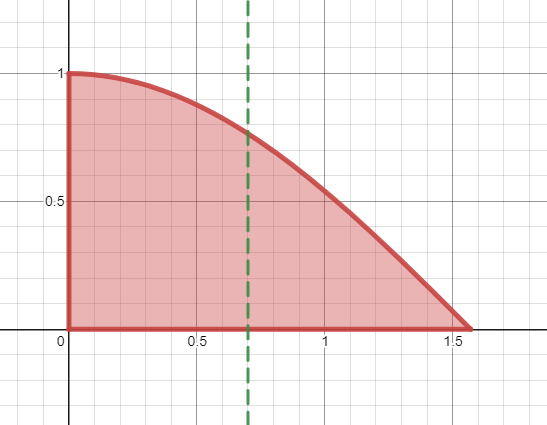
\Bigl\{ (x,y) \text{ tels que } 0 \le x \le \frac{\pi}{2} \text{ et } 0 \le y \le \cos(x) \Bigr\}
\end{equation*}
(c'est une partie de l'orthant positif délimitée par un arc de cosinus).
On trace à présent la droite verticale d'équation \(x=S\) où \(S\) est un paramètre à déterminer.
