Now that we can find all the nodes that are reachable from a given node, we are going to see how we can compute connected components of an undirected graph.
As the name suggests, the connected components of an undirected graph are the parts of the graph that are connected together, that is, the parts for which any two nodes have at least one path between them.
Example:
The following figure shows a graph on the left and its connected components on the right. Nodes on the same component are colored with the same color.
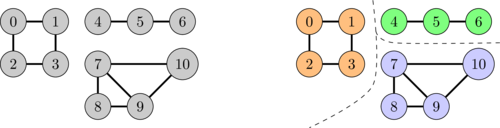
On the above graph, if we call BFS on node 0 we will visit nodes 0, 1, 2 and 3. In general, when we call BFS on node \(u\), it will visit the whole connected component of \(u\). Therefore we can compute all the connected components by keeping a global visited set and looping over the nodes of the graph and calling BFS for each unvisited node. Each call to BFS will visit a new connected component and we will avoid to vist the same connected component twice because the visited set will be global.
One way to represent the components is to have an array \(comp\) such that \(comp[u] = comp[v]\) if and only if nodes \(u\) and \(v\) are one the same connected component. We can achieve this by labelling all nodes of each BFS visit with an id \(compId\) that we increment every time that we start a new BFS.
The following animation illustrates this process.
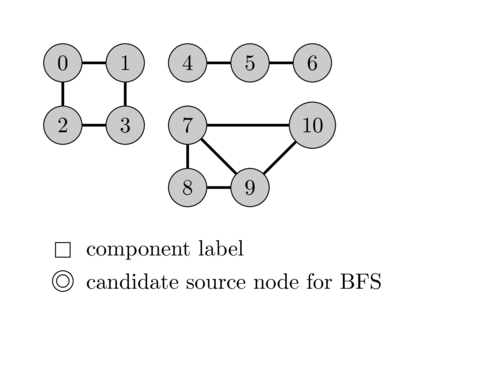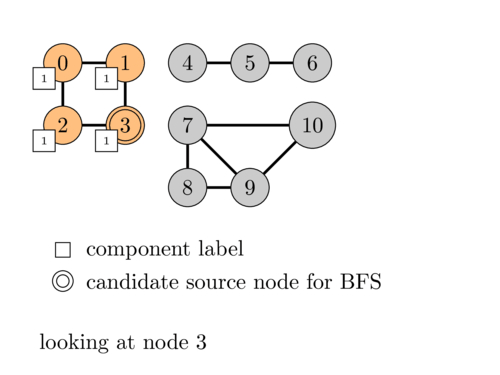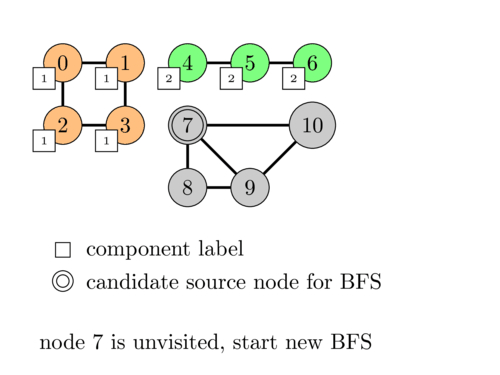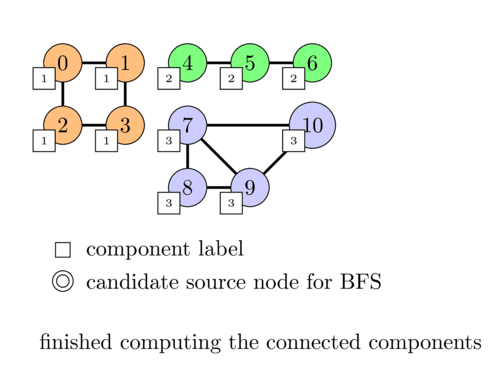
In terms of code it consists simply of adding a loop around our BFS code to try all nodes and adding the \(comp\) array to keep track of the component of each node.
static Integer[] connectedComponents(LinkedList<Integer>[] g) {
Integer[] comp = new Integer[g.length];
int compId = 0;
for(int s = 0; s < g.length; s++) {
// check is s is already labeled
if(comp[s] != null) continue;
// s is not labeled, perform a BFS from it to compute its component
// initialize the queue and visited set
Queue<Integer> Q = new LinkedList<>();
Q.add(s);
// set the component of s
comp[s] = compId;
// loop while there are nodes in the queue to process
while(!Q.isEmpty()) {
int u = Q.poll();
// we are now processing node u
for(int v : g[u]) {
// visit edge (u, v)
if(comp[v] == null) {
// node v has not yet been visited, add it
Q.add(v);
// set the component of v
comp[v] = compId;
}
}
}
// finished labelling the component, increment the component id
compId += 1;
}
return comp;
}
 INGInious
INGInious