Quelle est l'aire de cette ellipse ? (1)

On considère dans le plan une ellipse d'équation $x^2 + 2y^2 = 1$ .

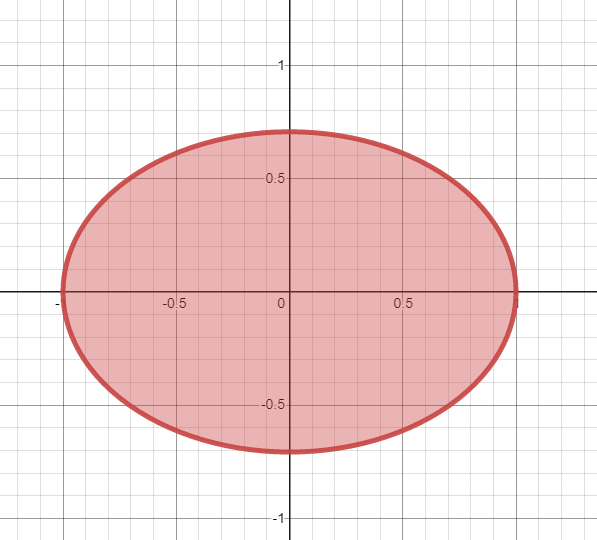
Dans ce problème, on cherche à calculer l'aire de la région du plan délimitée par cette ellipse.

Considèrons la fonction $f(x)=\sqrt{\frac{1-x^2}{2}}$ définie sur le domaine $[-1,1]$ .

Il n'est pas difficile de se convaincre que la région comprise entre le graphe de cette fonction et l'axe $Ox$ (l'aire "sous la courbe") est exactement la moitié de l'ellipse ci-dessus (c'est dû au fait que $y = f(x) \Leftrightarrow x^2 + 2 y^2 = 1 \text{ pour tout } y\ge0$ ).

On sait de plus que l'aire de cette région peut s'écrire $\int_{-1}^1 f(x) \ \mathrm{d}x$ .

Cole este comando no seu terminal:

A senha para conectar é

Questão 1: Une substitution

Hint Add answer

Pour calculer l'intégrale définie $\int_{-1}^1 f(x) \ \mathrm{d}x$ il est recommandé d'effectuer la substitution trigonométrique $x=\sin t$ .

Après cette substitution cette intégrale définie devient $\int_{-M}^M g(t)\ \mathrm{d}t$ où $M$ est une constante à déterminer, et $g(t)$ est une certaine fonction de $t$ .

Que vaut $g(t)$ ?

Format example : expression: 5x+3 equation: x=y+3 inequation: x<2y+1

Questão 2:

Add answer

Que vaut la constante $M$ ?

Format example : expression: 5x+3 equation: x=y+3 inequation: x<2y+1

Questão 3: Calcul de l'aire de l'ellipse

Hint Add answer

En vous aidant de ce qui précède, calculez l'aire de cette ellipse.

Format example : expression: 5x+3 equation: x=y+3 inequation: x<2y+1

Prazo de entrega	14/09/2024 17:00:00
Limite de submissão	3 submissões

Informações

Entrar