Jusqu'à présent, les valeurs des neurones sont assez arbitraires, leurs valeurs dans l'absolu ne signifient rien de particulier et elles n'ont pas de signification particulière.
Par exemple : est-ce qu'une valeur de 56 est grande ? Ca dépend : si les autres valeurs sont 3 et 5 alors oui, mais si elles sont de 1996 et 2019 alors non.
Pour cela on va utiliser une fonction d'activation, l'idée étant de restreindre les valeurs dans un certain intervalle (par exemple entre 0 et 1).
Il existe diverses fonctions d'activation que l'on peut utiliser, mais la plus utilisée est la sigmoïde.
Son équation est la suivante : \(f(x) = \frac{1}{1+e^{-x}}\) . Son graphique est le suivant
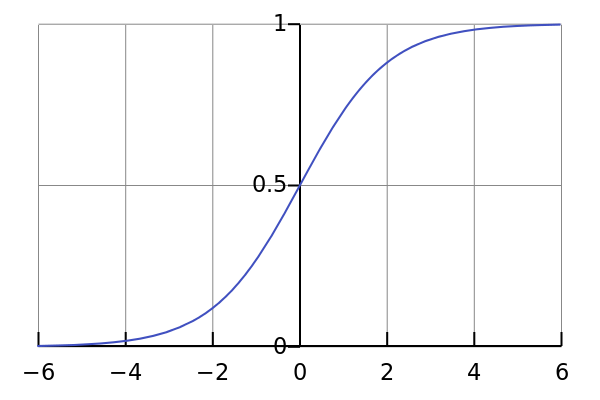
Cette fonction comporte de nombreux avantages, mais ici ce qui va nous intéresser c'est qu'elle permet de transformer nos valeurs pour les mettre entre 0 et 1.
En l'appliquant successivement sur tous les neurones calculés, tu verras qu'à la fin on aura les probabilités liées à chaque conclusion au lieu d'avoir une valeur arbitraire.
Par exemple en l'appliquant sur l'exemple de l'exercice précédent, qui avait comme valeur de neurones de sorties (56, -56), on obtient maintenant (92%, 8%) qui signifie que le réseau pense à 92% que c'est une ligne verticale.
Ci-dessous, une mini-calculatrice qui calculera pour toi la sigmoïde du nombre indiqué dans la barre
Objectif
Pour les exercices qui vont suivre, on va s'interesser à l'utilité de la fonction d'activation pour l'image
 INGInious
INGInious