One of the main uses of cross product is in determining the relative position of points and other objects. For this, we define the function \(orient(A, B, C) = \vec{AB} \times \vec{AC}\). It is positive if \(C\) is on the left side of \(\vec{AB}\), negative on the right side, and zero if \(C\) is on the line containing \(\vec{AB}\).
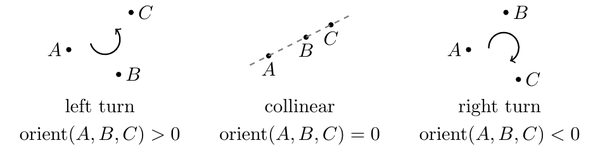
It is straightforward to implement:
// create the vector from point a to point b
static Point vec(Point a, Point b) {
return new Point(b.x - a.x, b.y - a.y);
}
static double orient(Point a, Point b, Point c) {
return cross(vec(a, b), vec(a, c));
}
In most situations we only care about the sign of \(orient(a, b, c)\). Therefore we define a function \(sorient(a, b, c)\) which returns the sign of \(orient(a, b, c)\)
\begin{equation*}
sorient(a, b, c) =
\begin{cases}
1 & \quad orient(a, b, c) > 0 \\
0 & \quad orient(a, b, c) = 0 \\
-1 & \quad orient(a, b, c) < 0
\end{cases}
\end{equation*}
static double sorient(Point a, Point b, Point c) {
double o = orient(a, b, c);
return o < 0 ? -1 : o > 0 ? 1 : 0;
}
 INGInious
INGInious